Question

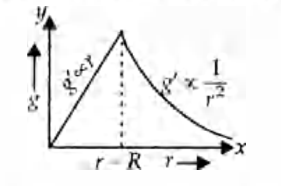
The dependence of acceleration due to gravity $g$ on the distance $r$ from the centre of the earth, assumed to be a sphere of radius $R$ of uniform density is as shown in figures below

The correct figure is

• A. $(i)$
• B. $(ii)$
• C. $(iii)$
• D. $(iv)$

Answer 1

Answer: (D)

The acceleration due to gravity at a depth $d$ below surface of earth is
$g^{\prime}=\frac{G M}{R^{2}}\left(1-\frac{d}{R}\right)=g\left(1-\frac{d}{R}\right)$
$g^{\prime}=0$ at $d=R$.
i.e., acceleration due to gravity is zero at the centre of earth.
Thus, the variation in value $g$ with $r$ is
For, $r>R$
$g^{\prime}=\frac{g}{\left(1+\frac{h}{R}\right)^{2}}=\frac{g R^{2}}{r^{2}}$
$ \Rightarrow g^{\prime} \propto \frac{1}{r^{2}}$
Here, $R+h=r$
For $r< R, g^{\prime}=g\left(1-\frac{d}{R}\right)=\frac{g^{r}}{R}$
Here, $R-d=r \Rightarrow g^{\prime} \propto r$
Therefore, the variation of $g$ with distance from centre of the earth will be as shown in the figure.