Question

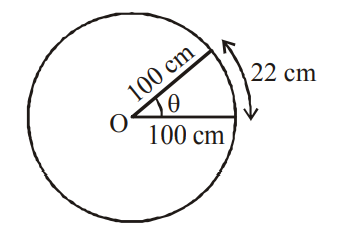
The degree measure of the angle subtended at the centre of a circle of radius $100 \,cm$ by an arc of length $22 \,cm$ as shown in figure, is $\left[\right.$ Use $\left.\pi=\frac{22}{7}\right]$

• A. $12^{\circ} 30'$
• B. $12^{\circ} 36'$
• C. $11^{\circ} 36'$
• D. $11^{\circ} 12'$

Answer 1

Answer: (B)

Given radius, $r =100\, cm$ and arc length, $l=22 \,cm$
We know that, $l= r \theta ; \theta=\frac{l}{ r }=\frac{\text { Arc length }}{\text { Radius }}$
$=\frac{22}{100}=0.22 \,rad =0.22 \times \frac{180}{\pi}$ degree
$=0.22 \times \frac{180 \times 7}{22}=\frac{22}{100} \times \frac{180 \times 7}{22}$
$=\frac{126}{10}=12 \frac{6^{\circ}}{10}=12^{\circ}+\frac{6}{10} \times 60' \left[\because 1^{\circ}=60'\right]$
$=12^{\circ}+36'=12^{\circ} 36'$
Hence, the degree measure of the required angle is $12^{\circ} 36'$.