1. Tardigrade
  2. Question
  3. Mathematics
  4. The curve y=(|x|-1) operatornamesgn(x-1) divides (9 x2/64)+(4 y2/25)=(1/π) into two parts of areas A1 and A2 ( A 1< A 2), then [Note: operatornamesgn( k ) denotes signum function of k.]

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

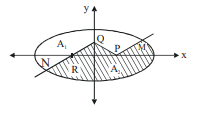
Q. The curve $y=(|x|-1) \operatorname{sgn}(x-1)$ divides $\frac{9 x^2}{64}+\frac{4 y^2}{25}=\frac{1}{\pi}$ into two parts of areas $A_1$ and $A_2$ $\left( A _1< A _2\right)$, then
[Note: $\operatorname{sgn}( k )$ denotes signum function of $k$.]

Conic Sections

Solution:

Area of an ellipse $=\pi ab =\frac{20}{3}$, Area of triangle $P Q R=1$
$\therefore A _1=\frac{7}{3} ; A _2=\frac{13}{3} $ [By symmetry area $M =$ area $N$ ]

Solution Image