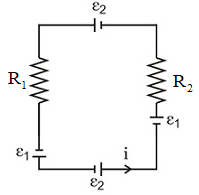
Q.
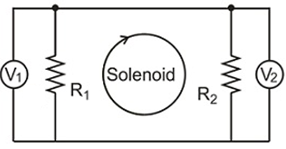
The current through the solenoid is changing in such way that flux through it is given by $\phi = \epsilon \text{t}$ . The solenoid is surrounded by a loop having resistance $\text{R}_{\text{1}}$ and $\text{R}_{\text{2}}$ as shown. Then the reading of the two voltmeters $V_{1}$ and $V_{2}$ differ by :
NTA AbhyasNTA Abhyas 2020
Solution: