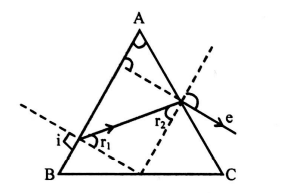
Question

The cross-section of a prism $(\mu=1.5)$ in an equilateral triangle. A ray of light is incident perpendicular on one of the faces. Find the angle of deviation (in degree) of the ray.

Answer 1

Here $I =90^{\circ}$
So $S=i+ e- A$
$=90^{\circ}+ e - A$
However when $I =90^{\circ}$
for "$AB$"
$1 \times \sin 90^{\circ} =\mu \sin r_{1}$
$\sin r _{1}=\frac{1}{\mu}=\frac{1}{1.5}=\frac{2}{3}$
$r _{1}=\sin ^{-1}\left(\frac{2}{3}\right) $
$r _{1}=\theta_{ c }$
So $ \theta_{c}=\sin ^{-1}\left(\frac{2}{3}\right)$
Now for '$AC$'
$\mu \sin r _{2}=1 \sin e$
$\sin e=\mu \sin \left(A-\theta_{c}\right)$
$e=\sin ^{-1}\left[\mu \sin \left(A-\theta_{c}\right)\right]$
$=\sin ^{-1}\left[1.5 \sin \left(90^{\circ}-\sin ^{-1} 2 / 3\right)\right]$
$ e=29^{\circ} $
so $ \delta_{\max }= 90^{\circ}+29-60^{\circ}$
$\left(\text { Here } A=60^{\circ}\right)$
$\delta_{\max }= 59 $