1. Tardigrade
  2. Question
  3. Mathematics
  4. The coordinates of the orthocenter of the triangle that has the coordinates of midpoints of its sides as (0,0), (1,2) and (- 6 ,3) is

Question Error Report

Thank you for reporting, we will resolve it shortly

Back to Question

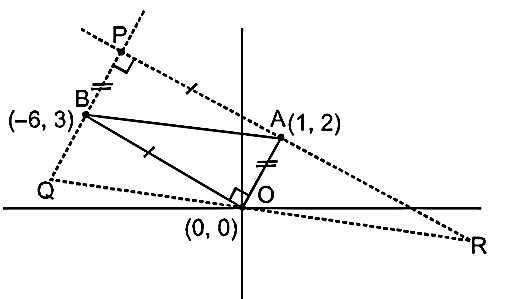
Q. The coordinates of the orthocenter of the triangle that has the coordinates of midpoints of its sides as $\left(0,0\right), \, \left(1,2\right)$ and $\left(- 6 ,3\right)$ is

NTA AbhyasNTA Abhyas 2020Straight Lines

Solution:

Line joining the midpoints of two sides is $\parallel$ to the third side and half of it.
$\angle O=90^{o}$ (as $AO\bot OB$ )
Hence $P$ will be the orthocentre
Solution
$AOBP$ forms a rectangle.
$\therefore \, \, P=A+B-O$ (using the concept that diagonals bisect each other)
$P(x, y)=\left[\begin{array}{c}x=-6+1-0=-5 \\ y=2+3-0=5\end{array}\right.$