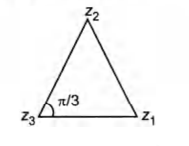
Question

The complex numbers $z_1, z_2$ and $z_3$ satisfying $\frac{z_1-z_3}{z_2-z_3}=\frac{1-i \sqrt 3}{2}$ are the vertices of a triangle which is

• A. of area zero
• B. right angled isosceles
• C. equilateral
• D. obtuse angled isosceles

Answer 1

Answer: (C)

$\frac{z_{1}-z_{3}}{z_{2}-z_{3}} =\frac{1-i \sqrt{3}}{2}=\frac{(1-i \sqrt{3})(1+i \sqrt{3})}{2(1+i \sqrt{3})} $
$=\frac{1-i^{2} 3}{2(1+i \sqrt{3})}=\frac{4}{2(1+i \sqrt{3})}=\frac{2}{(1+i \sqrt{3})} $
$\Rightarrow \frac{z_{2}-z_{3}}{z_{1}-z_{3}}=\frac{1+i \sqrt{3}}{2}=\cos \frac{\pi}{3}+i \sin \frac{\pi}{3} $
$\Rightarrow\left|\frac{z_{2}-z_{3}}{z_{1}-z_{3}}\right|=1 $ and $ \arg \left(\frac{z_{2}-z_{3}}{z_{1}-z_{3}}\right)=\frac{\pi}{3}$
Hence, the triangle is an equilateral.

Alternate Solution
$\therefore \frac{z_{1}-z_{3}}{z_{2}-z_{3}}=\frac{1-i \sqrt{3}}{2}$
$\Rightarrow \frac{z_{2}-z_{3}}{z_{1}-z_{3}}=\frac{2}{1-i \sqrt{3}}=\frac{1+i \sqrt{3}}{2}=\cos \frac{\pi}{3}+i \sin \frac{\pi}{3} $
$\Rightarrow \arg \left(\frac{z_{2}-z_{3}}{z_{1}-z_{3}}\right)=\frac{\pi}{3} $ and also $\left|\frac{z_{2}-z_{3}}{z_{1}-z_{3}}\right|=1$
Therefore, triangle is equilateral.