Q.
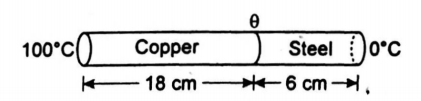
The coefficient of thermal conductivity of copper is nine times that of steel. In the composite cylindrical bar shown in the figure, what will be the temperature at the junction of copper and steel?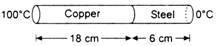
BHUBHU 2004
Solution: