Question

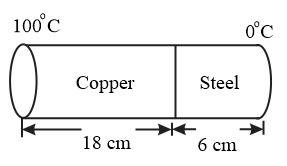
The coefficient of thermal conductivity of copper is $9$ times that of steel. In the composite cylindrical bar shown in the figure, what will be the temperature at the junction of copper and steel?

• A. $75^\circ C$
• B. $67^\circ C$
• C. $25^\circ C$
• D. $33^\circ C$

Answer 1

Answer: (A)

Temperature of the interface,
$\theta =\frac{K_{1} \theta _{1} l_{2} + K_{2} \theta _{2} l_{1}}{K_{1} l_{2} + K_{2} l_{1}}$
It is given that $K_{Cu}=9K_{s}$ . So, if $K_{s}=K_{1}=K$ , then
$K_{Cu}=K_{2}=9K$
$\Rightarrow $ $\theta =\frac{9 K \times 100 \times 6 + K \times 0 \times 18}{9 K \times 6 + K \times 18}$
$ \, =\frac{5400 K}{72 K}=75^\circ C$