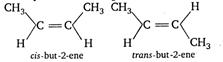
Q. The $ cis $ and trans isomers are represented by
VMMC MedicalVMMC Medical 2007
Solution:
Key Idea: The geometrical isomers must have (i) At least one carbon-carbon double bond. (ii)The two groups attached to same carbon atom should be different. Geometrical isomers exists in two structural forms-cis and trans. In cis form the two groups are present on the same side and in trans form in which the two same groups are present on different sides. The isomer which forms cis and trans structure, will show geometrical isomerism. Draw all the choices to find which of them will show geometrical isomerism. $ C{{H}_{3}}-C{{H}_{2}}-\underset{\text{pent}\,-1-\text{ene}}{\mathop{C{{H}_{2}}}}\,-CH=C{{H}_{2}} $ $ \underset{\text{prop}-1-\text{ene}}{\mathop{C{{H}_{3}}-CH=C{{H}_{2}}}}\, $ $ \underset{\text{but}\,-1-\,\text{ene}}{\mathop{C{{H}_{3}}-C{{H}_{2}}-CH=C{{H}_{2}}}}\, $ $ \because $ choice (a), (c) and (d) have two identical groups (hydrogen) attached to double bonded carbon atoms. $ \therefore $ They dont exhibit geometrical isomerism
$ \therefore $ choice (b) will show geometrical isomerism.