Question

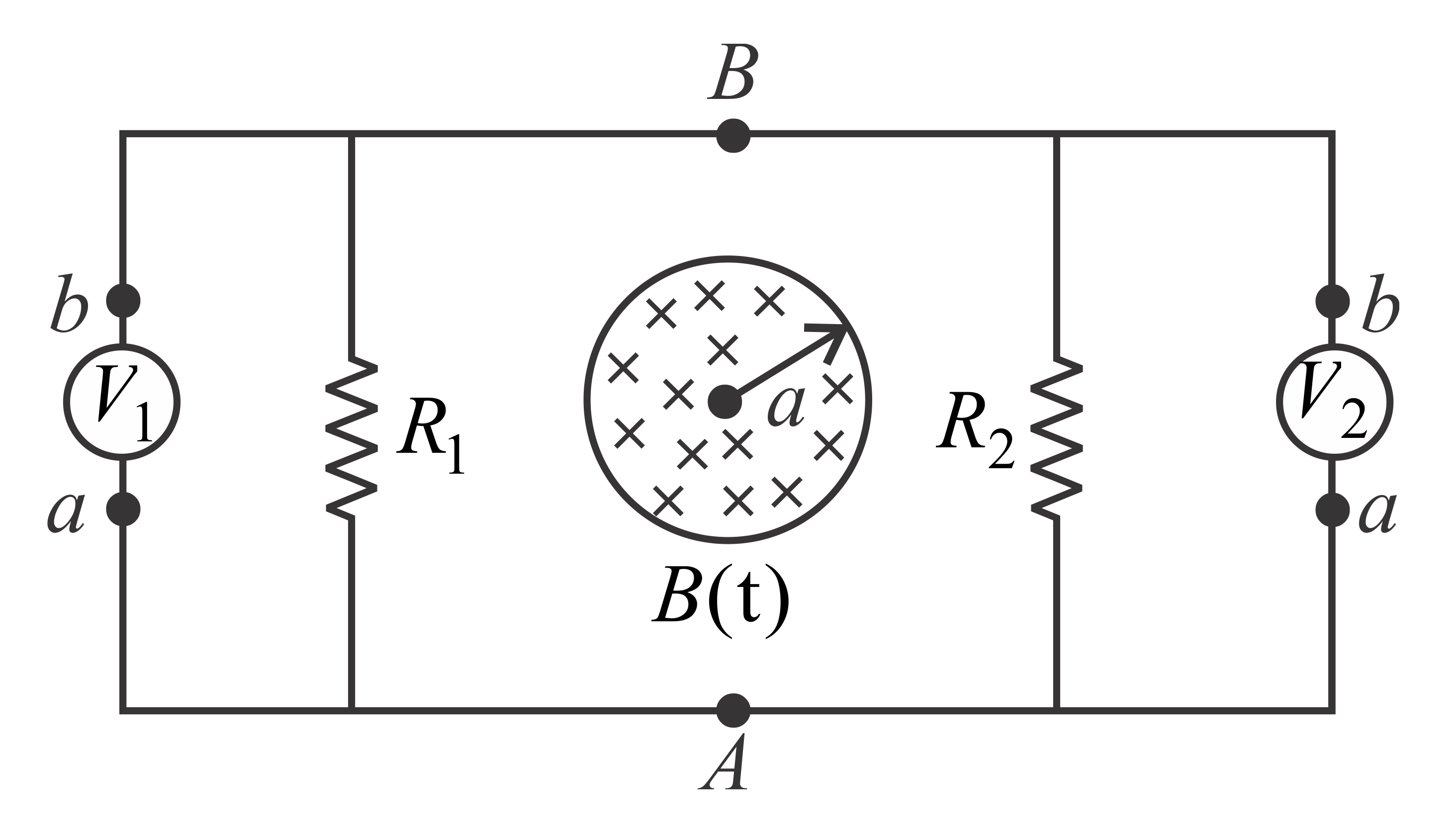
The circuit shown in the figure consists of two resistances $R_{1}$ & $R_{2}$ connected to two ideal voltmetres $V_{1}$ & $V_{2}$ . Assume that a voltmeter reads $\Delta V=-\int\limits _{a}^{b}\vec{E}.d\vec{l}$ between its terminals. A time-varying magnetic field $B\left(\right.t\left.\right)=B_{0}t$ (where $B_{0}$ is a positive constant of proper dimensions and $t$ is time) exists in a circular region of radius a and it is directed into the plane of the figure. The reading of voltmeter $V_{2}$ is

• A. $\frac{\pi a^{2} B_{0} R_{1}}{R_{1} + R_{2}}$
• B. $-\frac{\pi a^{2} B_{0} R_{2}}{R_{1} + R_{2}}$
• C. $-\frac{\pi a^{2} B_{0} R_{1}}{R_{1} + R_{2}}$
• D. $\frac{\pi a^{2} B_{0} R_{2}}{R_{1} + R_{2}}$

Answer 1

Answer: (B)

$\phi=\pi a^{2}B_{0}t$
$\epsilon =-\frac{d \phi}{d t}$
$\Rightarrow \epsilon =\pi a^{2}B_{0}$ (induced emf)
$i=\frac{\pi a^{2} B_{0}}{R_{1} + R_{2}}$ (induced current)
$\Delta V_{1}=-\int\limits _{a}^{b}\vec{E}\cdot d\vec{l}=-\left(- i R_{1}\right)=\frac{\pi a^{2} B_{0} R_{1}}{R_{1} + R_{2}}$
$\Delta V_{2}=-\int\limits _{a}^{b}\vec{E}\cdot d\vec{l}=-\left(i R_{2}\right)=-\frac{\pi a^{2} B_{0} R_{2}}{R_{1} + R_{2}}$