Q.
The capacitance of a parallel plate capacitor with plate area A and separation $d$, is $C$. The space between the plates is filled with two wedges of dielectric constants $K_1 $ and $K_2 $ respectively (figure). Find the capacitance of the resulting capacitor.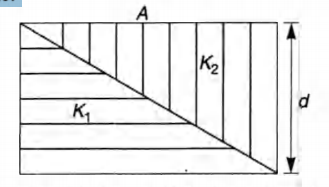
IIT JEEIIT JEE 1996Electrostatic Potential and Capacitance
Solution:
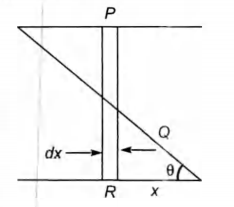
Let length and breadth of the capacitor be / and b respectively and $d$ be the distance between the plates as shown in figure. Then, consider a strip at a distance $x$ of width $d x$.
Now, $Q R=x \tan \theta$
and $P Q=d-x \tan \theta$
Where $\tan \theta=d / l$
Capacitance of $PQ$
$C_{1}=\frac{K_{1} \varepsilon_{0}(b d x)}{d-x \tan \theta}=\frac{K_{1} \varepsilon_{0}(b d x)}{d-\frac{x d}{l}}$
$C_{1}=\frac{K_{1} \varepsilon_{0}(b l d x)}{d(1-x)}=\frac{K_{1} \varepsilon_{0} A(d x)}{d(1-x)}$
and $C 2=$ capacitance of $Q R$
$=\frac{K_{2} \varepsilon_{0} b(d x)}{x \tan \theta}$
$C_{2}=\frac{K_{2} \varepsilon_{0} A(d x)}{x d}\left(\tan \theta=\frac{d}{l}\right)$
Now, $C_{1}$ and $C_{2}$ are in series. Therefore, their resultant capacity CO will be given by
$\frac{1}{C_{0}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}$
Then, $\frac{1}{C_{0}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}$
$=\frac{d(1-x)}{K_{1} \varepsilon_{0} A(d x)}+\frac{x . d}{K_{2} \varepsilon_{0} A(d x)}$
$\frac{1}{C_{0}}=\frac{d}{\varepsilon_{0} A(d x)}\left(\frac{1-x}{K_{1}}+\frac{x}{K_{2}}\right)$
$=\frac{d\left\{K_{2}(l-x)+K_{1} x\right\}}{\varepsilon_{0} A K_{1} K_{2}(d x)}$
$\therefore C_{0}=\frac{\varepsilon_{0} A K_{1} K_{2}}{d\left\{K_{2}(l-x)+K_{1} x\right\}} d x$
$C_{0}=\frac{\varepsilon_{0} A K_{1} K_{2}}{d\left\{K_{2} l+\left(K_{1}-K_{2}\right) x\right\}} d x$
Now, the net capacitance of the given parallel plate capacitor is obtained by adding such infinitesimal capacitors placed parallel from $x=0$ to $x=1$
i.e. $C_{R}=\int\limits_{x=0}^{x=1} C_{0}=\int\limits_{0}^{1} \frac{\varepsilon_{0} A K_{1} K_{2}}{d\left\{K_{2} l+\left(K_{1}-K_{2}\right) x\right\}} d x$
Finally we get $C_{R}=\frac{K_{1} K_{2} \varepsilon_{0} A}{\left(K_{2}-K_{1}\right) d}$ In $\frac{K_{2}}{K_{1}}$
$=\frac{C K_{1} K_{2}}{K_{2}-K_{1}}$ In $\frac{K_{2}}{K_{1}},$ where $E=\frac{E d}{l}$