Question

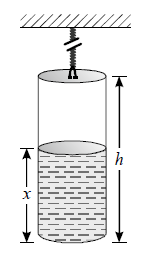
The bob of a simple pendulum, which is in the shape of a hollow cylinder of mass $M$, radius $r$ and length $h$ is suspended by a long string (the mass of the base and lid of the cylinder are negligible). The cylinder is filled with a liquid of density $\rho$ upto a height of $x$. Then the value of $x$ for which the time period of the pendulum is maximum, is given by which of the following equations: $\left(\lambda=\pi r^{2} \rho\right)$

• A. $\lambda x^{2}-2 M x+M h=0$
• B. $\lambda x^{2}+2 M x+M h=0$
• C. $x=H / 2$
• D. $\lambda x^{2}+2 M x-M h=0$

Answer 1

Answer: (D)

Centre of mass of system is
$x_{c m}=\frac{(\lambda x) \frac{x}{2}+M\left(\frac{h}{2}\right)}{M+\lambda x}$
Time period is maximum when
$\frac{d x_{c m}}{d x}=0$
$\Rightarrow (M+\lambda x) \lambda x-\left(\frac{\lambda x^{2}}{2}+\frac{M h}{2}\right) \lambda=0 $
$\left(M x+\lambda x^{2}\right)-\frac{\lambda x^{2}}{2}-\frac{M h}{2}=0$
$\lambda x^{2}+2 M x-M h=0$