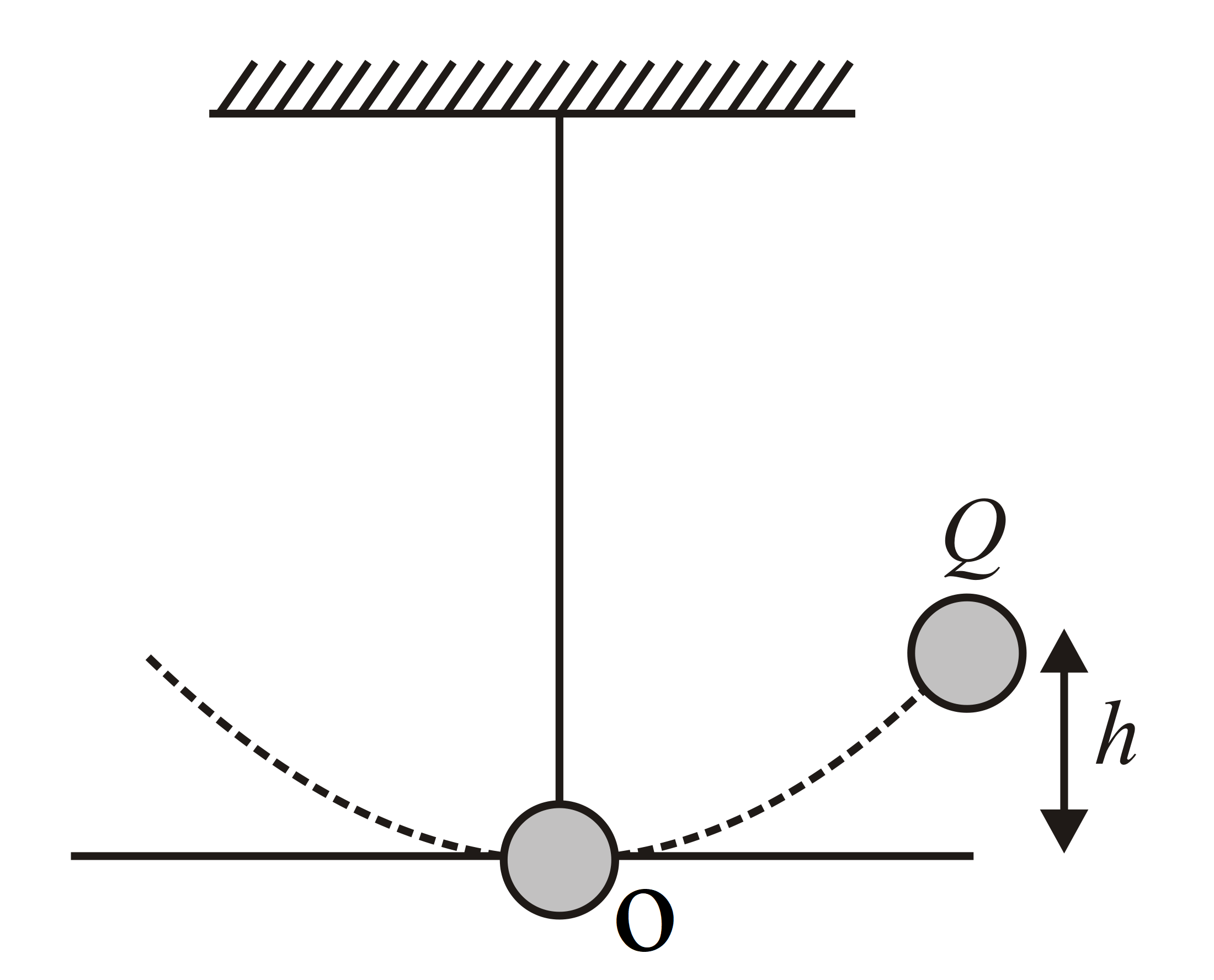
Question

The bob of a simple pendulum is displaced from its equilibrium position, $O$ to a position, $Q$ which is at height, $h$ above $O$ and then, the bob is then released. Calculate the tension in the string if the bob passes through $O$ if mass of the bob is $m$ and time period of oscillations is $2s$ .

• A. $m\left(g + \pi \sqrt{2 g h}\right)$
• B. $m\left(g + \sqrt{\left(\pi \right)^{2} g h}\right)$
• C. $m\left(g + \sqrt{\frac{\left(\pi \right)^{2}}{2} g h}\right)$
• D. $m\left(g + \sqrt{\frac{\left(\pi \right)^{2}}{3} g h}\right)$

Answer 1

Answer: (A)

Tension in the string when bob passes through lowest point
$T=mg+\frac{m v^{2}}{r}=mg+mv\omega $ $\left[\because \, \, v = r \omega \right]$
Putting $v=\sqrt{2 g h}$ and $\omega =\frac{2 \pi }{T}=\frac{2 \pi }{2}=\pi $
We get $T=m\left(g + \pi \sqrt{2 g h}\right)$