Question

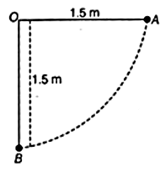
The bob of a pendulum is released from a horizontal position $A$ as shown in the figure. If the length of the pendulum is $1.5 \, m$ , what is the speed with which the bob arrives at the lowermost point $B$ , given that it dissipated $5\%$ of its initial energy against air resistance?

• A. $5ms^{- 1}$
• B. $5.5 \, m \, s^{- 1}$
• C. $5.3 \, m \, s^{- 1}$
• D. $4.4 \, m \, s^{- 1}$

Answer 1

Answer: (C)

At the point $A$ the energy of the pendulum is entirely potential energy. At point B, the energy of the pendulum is entirely kinetic energy. It means that as the bob pendulum lowers from A to B, the potential energy is converted into kinetic energy. Thus, at $B$ , KE = PE. But $5\%$ of the potential energy is dissipated against air resistance.

$KE$ at $B=95\%of \, PE \, at \, A$ .... (i)
$\therefore \, \, \, $ From equation (i), $\frac{1}{2}mv^{2}=\frac{95}{100}mgh$
$v^{2}=2\times \frac{95}{100}gh=2\times \frac{95}{100}\times 9.8\times 1.5$
$v=\sqrt{\frac{19 \times 9.8 \times 1.5}{10}}=\sqrt{27.93}=5.285 \, ms^{- 1}$
$v=5.3 \, ms^{- 1}$