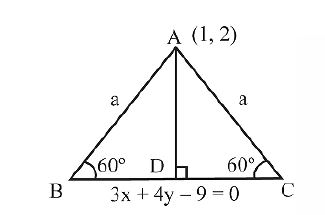
Q. The base of an equilateral triangle is along the line given by $3x + 4y = 9$. If a vertex of the triangle is $(1, 2)$, then the length of a side of the triangle is :
Solution:
Let BC is base of equilater triangle ABC with side a and A (1, 2)
AD = a sin $60^{\circ}$
AD is perpendicular distance of PtA from line $3x + 4y - 9 = 0$
AD $= \left|\frac{3\times1+4\times2-9}{\sqrt{3^{2}+4^{2}}}\right|$
a sin $60^{\circ} =\frac{2}{5}$
$a = \frac{4}{5\sqrt{3}} = \frac{4\sqrt{3}}{15}$