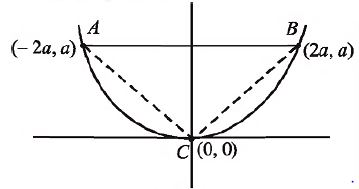
Q. The area of triangle formed by the lines joining the vertex of the parabola, $x^2 = 8y$, to the extremities of its latus rectum is
AIEEEAIEEE 2012Determinants
Solution:
Given parabola is $x^2 = 8y$
$\Rightarrow 4a = 8 \Rightarrow a=2$
To find: Area of $\Delta ABC$
$A = \left(-2a, a\right)=\left(-4,2\right)$
$B=\left(2a, a\right)=\left(4,2\right)$
$C=\left(0,0\right)$
$\therefore \,$ Area $= \frac{1}{2}\begin{vmatrix}-4&2&1\\ 4&2&1\\ 0&0&1\end{vmatrix}$
$= \frac{1}{2}\left[-4\left(2\right)-2\left(4\right)+1\left(0\right)\right]$
$= \frac{-16}{2} = -8 \approx\, 8 \,sq.$ unit
($\because\,$ area cannot be negative)