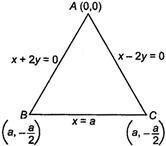
Question

The area of the triangle formed by the lines $ {{x}^{2}}-4{{y}^{2}}=0 $ and $ x=a $ , is

• A. $ 2{{a}^{2}} $
• B. $ \frac{{{a}^{2}}}{2} $
• C. $ \frac{\sqrt{3}{{a}^{2}}}{2} $
• D. $ \frac{2{{a}^{2}}}{\sqrt{3}} $

Answer 1

Answer: (B)

Given lines are $ {{x}^{2}}-4{{y}^{2}}=0 $
$ \Rightarrow $ $ (x-2y)(x+2y)=0 $
$ \Rightarrow $ $ (x-2y)=0,\,\,(x+2y)=0 $ and $ x=a $
On drawing these lines, we get the following triangle
Here, $ A(0,\,\,0),\,\,B\left( a,\,\,-\frac{a}{2} \right) $ and $ C\left( a,\,\,\frac{a}{2} \right) $ are the vertices of triangle.
$ \therefore $ Required area $ =\frac{1}{2}\left| \begin{matrix} 0 & 0 & 1 \\ a & -\frac{a}{2} & 1 \\ a & \frac{a}{2} & 1 \\ \end{matrix} \right| $
$ =\frac{1}{2}\left[ a\times \frac{a}{2}+a\times \frac{a}{2} \right] $
$ =\frac{{{a}^{2}}}{2}sq\,\,unit $