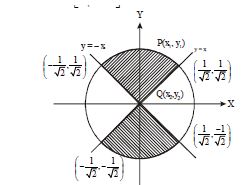
Q. The area of the region $R=\{(x, y):|x| \leq|y|$ and $\left.x^{2}+y^{2} \leq 1\right\}$ is
BITSATBITSAT 2015
Solution:
Required area $=4$ (Area of the shaded region in first quadrant)
$=4 \int\limits_{0}^{1 \sqrt{2}}\left(y_{1}-y_{2}\right) d x=4 \int\limits_{0}^{1 \sqrt{2}}\left(\sqrt{1-x^{2}}-x\right) d x$
$=4\left[\frac{x}{2} \sqrt{1-x^{2}}+\frac{1}{2} \sin ^{-1} x-\frac{x^{2}}{2}\right]^{1 / \sqrt{2}}$
$=4\left[\frac{1}{2 \sqrt{2}} \times \frac{1}{\sqrt{2}}+\frac{1}{2} \times \frac{\pi}{4}-\frac{1}{4}\right]$
$=4\left[\frac{1}{4}+\frac{\pi}{8}-\frac{1}{4}\right]$
$=\frac{4 \pi}{8}=\frac{\pi}{2}$ sq units