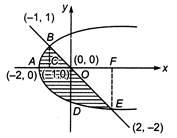
Q. The area of the plane region bounded by the curve $ x={{y}^{2}}-2 $ and the line $ y=-x $ is (in square units)
Solution:
Given curves $ x={{y}^{2}}-2 $ and $ y=x $
Thus, interection point are $ (-1,1) $ and $ (2,-2) $ We are to find the area of shaded part Area of $ ABC=\int_{-2}^{-1}{\sqrt{x+2}}dx $
$=\left[ \frac{2}{3}{{(x+2)}^{3/2}} \right]_{-2}^{-1}=\frac{2}{3} $ sq unit Area of $ BCO=\int_{-1}^{0}{-x}\,dx=\left( -\frac{{{x}^{2}}}{2} \right)_{-1}^{0} $
$=\frac{1}{2}sq\text{ }unit $ Area of ADO
$=\int_{-2}^{0}{\sqrt{x+2}}dx=\left[ \frac{2}{3}{{(x+2)}^{3/2}} \right]_{-2}^{0} $
$=\frac{4}{3}\sqrt{2} $ Area of, $ ODE=area\text{ }of\text{ }ODEF-are\text{ }of\text{ }OFE $ $ \int_{0}^{2}{\sqrt{x+2}}dx-\int_{0}^{2}{(-x)}dx $
$=\left\{ \frac{2}{3}{{(x+2)}^{3/2}} \right\}_{0}^{2}-\left( -\frac{{{x}^{2}}}{2} \right)_{0}^{2} $
$=\left( \frac{16}{3}-\frac{4\sqrt{2}}{3} \right)-(2) $ (neglecting the negative sign)
$=\left( \frac{16}{3}-\frac{4\sqrt{2}}{3} \right)-(2) $
$ \therefore $ Required area
$=\frac{2}{3}+\frac{1}{2}+\frac{4\sqrt{2}}{3}+\frac{16}{3}-\frac{4\sqrt{2}}{3}-2 $
$=\frac{2}{3}+\frac{1}{2}+\frac{16}{3}-2 $
$=\frac{27}{6}=\frac{9}{2}sq.\,unit $