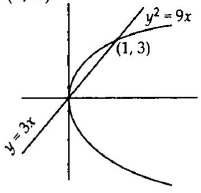
Q. The area in square units of the region bounded by $y^2 = 9x$ and $y = 3x$ is
Solution:
Intersecting points of $y^2 = 9x$ and $y = 3x$ is $(0, 0)$ and $(1, 3)$.
$ \therefore $ Required Area = $ \int\limits_0^1 (\sqrt{9x} - 3x) dx$
$= 3 \int\limits_0^1 \left(\sqrt{x} -x\right)dx=3\left[\frac{x^{3 /2}}{3/ 2} - \frac{x^{2}}{2}\right]^{1}_{0} $
$=3\left(\frac{2}{3} -\frac{1}{2}\right)=3\left(\frac{1}{6}\right)=\frac{1}{2}$ sq. unit