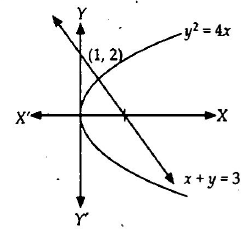
Q. The area in square units bounded by the normal at $(1, 2)$ to the parabola $y^2 = 4x, x$-axis and the curve is given by
Solution:
We have, $y^2 = 4x$
Differentiating w.r.t. $'x'$, we get
$2y \frac{dy}{dx} =4 \Rightarrow \frac{dy}{dx} = \frac{2}{y}$
$ \left(\frac{dy}{dx}\right)_{\left(1,2\right) } = \frac{2}{2} =1$
Equation of normal to the curve at (1, 2) is
$y -y_{1} = \frac{1}{\left(-\frac{dy}{dx}\right)} \left(x -x_{1}\right)$
$ \Rightarrow \left(y -2\right)=- \frac{1}{2}\left(x-1\right)$
$ \Rightarrow y -2 =-x +1$
$ \Rightarrow x+y =3$
The line $x + y = 3$ meets the $x$-axis at $x = 3$
$\therefore $ Required Area = $ \int\limits_0^1 \sqrt{4x} \, dx + \int\limits_1^3 (3-x) dx$
$= 2\left[\frac{x^{3 2}}{3 2}\right]^{1}_{0} +\left[3x -\frac{x^{2}}{2}\right]^{3}_{1} $
$=\frac{4}{3}\left(1\right) +\left[9 -\frac{9}{2}-3 +\frac{1}{2}\right]$
$ = \frac{4}{3}+\left(\frac{9}{2}-\frac{5}{2}\right)=\frac{4}{3}+\frac{4}{2}=\frac{4}{3}+2=\frac{10}{3} $ sq. units