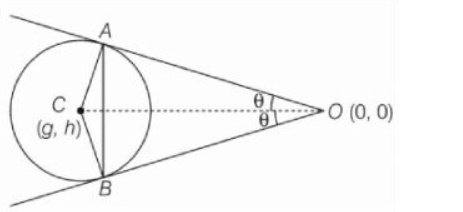
Question

The area (in sq. units) of the triangle formed by the two tangents drawn from the external point $O(0,0)$ to the circle $x^{2}+y^{2}-2 g x-2 h y+h^{2}=0$ and their chord of contact is

• A. $\frac{g h}{h^{3}+g^{2}}$
• B. $\frac{g h}{h^{2}+g^{3}}$
• C. $\frac{h g^{3}}{h^{2}+g^{2}}$
• D. $\frac{g h^{3}}{h^{2}+g^{2}}$

Answer 1

Answer: (D)

We have, equation of circle is
$x^{2}+y^{2}-2 g x-2 h y+h^{2}=0$
$\therefore $ Radius of circle,
$A C=\sqrt{g^{2}+h^{2}-h^{2}}=g$
and Length of tangent,
$O A=\sqrt{0+0-0-0+h^{2}}=h$
Now, in $\triangle O A C$
$\tan \theta=\frac{A C}{O A}=\frac{g}{h}$
$\therefore \sin \theta=\frac{2 \tan \theta}{1+\tan ^{2} \theta}=\frac{2 \times \frac{g}{h}}{1+\frac{g^{2}}{h^{2}}}=\frac{2 g h}{h^{2}+g^{2}}$
$\therefore $ Area of $\Delta O A B=\frac{1}{2} O A \times O B \times \sin 2 \theta$
$=\frac{1}{2} \times h \times h \times \frac{2 g h}{h^{2}+g^{2}}=\frac{g h^{3}}{h^{2}+g^{2}}$