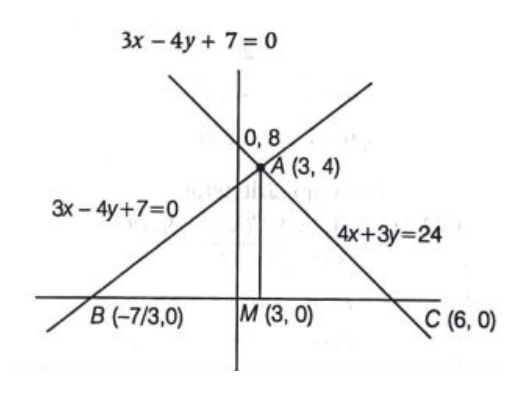
Question

The area ( in sq. units ) of the triangle formed by the tangent and normal drawn to the curves $\left(\frac{x}{3}\right)^{n}+\left(\frac{y}{4}\right)^{n}=2$ at $(3,4)$ and $X$-axis is

• A. $\frac{100}{3}$
• B. $48$
• C. $\frac{50}{3}$
• D. $144$

Answer 1

Answer: (C)

Equation of curve $\frac{x^{n}}{3^{n}}+\frac{y^{n}}{4^{n}}=2$
$\frac{n x^{n-1}}{3^{n}}+\frac{n y^{n-1}}{4^{n}} \frac{d y}{d x}=0$
$ \Rightarrow \frac{d y}{d x}=\frac{-4^{n} x^{n-1}}{3^{n} y^{n-1}}$
$\left(\frac{d y}{d x}\right)_{(3,4)}=\frac{-4^{n} \times 3^{n-1}}{3^{n} \times 4^{n-1}}=-\frac{4}{3}$
Slope of tangent is $-\frac{4}{3}$ and slope of normal $=\frac{3}{4}$
Equation of tangent of curve at $(3,4)$
$y-4=\frac{-4}{3}(x-3)$
$ \Rightarrow 3 y-12=-4 x+12$
$4 x+3 y=24$
Equation of normal of $(3,4)$

Area of triangle
$A B C=\frac{1}{2} \times B C \times A M$
$=\frac{1}{2} \times \frac{25}{3} \times 4=\frac{50}{3}$