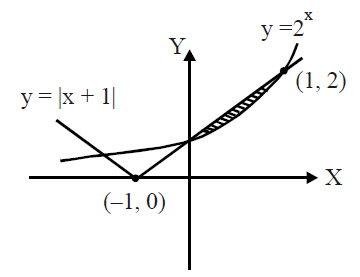Question

The area (in sq. units) of the region bounded by the curves $y = 2^x$ and $y = |x + 1|$, in the first quadrant is :

• A. $\frac{3}{2} - \frac{1}{\log_{e} 2} $
• B. $\frac{1}{2}$
• C. $ log_e 2+ \frac{3}{2}$
• D. $ \frac{3}{2}$

Answer 1

Answer: (A)

Required Area
$\int^{1}_{0} \left(\left(x+1\right)-2^{x}\right)dx $
$= \left(\frac{x^{2}}{2}+x - \frac{2^{x}}{In 2}\right)^{1}_{0} $
$ = \left(\frac{1}{2} + 1 - \frac{2}{In 2}\right) - \left(0+0 - \frac{1}{In 2}\right) $
$ = \frac{3}{2} - \frac{1}{In 2} $