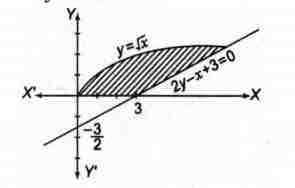
Q. The area (in sq units) bounded by the curves $y = \sqrt x , 2y-x+3=0$, X-axis and lying in the first quadrant, is:
Solution:
Given curves are $ y =\sqrt x \, \, \, \, ........(i) $
and $ 2 y - x + 3 = 0 \, \, ........(ii) $
On solving Eqs. (i) and (ii), we get
$\, \, \, \, \, \, \, 2\sqrt x - (\sqrt x)^2 + 3=0 $
$ \Rightarrow \, \, \, \, \, (\sqrt x)^2 - 2 \sqrt x - 3 = 0$
$ \Rightarrow \, \, \, \, \, (\sqrt x - 3) (\sqrt x + 1) = 0$
$ \Rightarrow \, \, \, \, \, \, \, \, \, \sqrt x = 3$
$ \Rightarrow \, \, \, \, \, \, \, \, \, \, [since, \sqrt x = -1 is not possible]$
$ \therefore \, \, \, \, \, \, \, \, \, \, \, y=3$
Hence, required area
$ \, \, \, \, \, \, \, \, \, \, = \int \limits_0^3 (x_2 - x_1) dy = \int \limits_0^3 {(2y+3) - y^2} dy $
$ \, \, \, \, \, \, \, \, \, \, = \Bigg [ y^2 + 3y - \frac{y^3}{3} \Bigg ]_0^3 = 9 + 9 - 9 = 9 sq units $