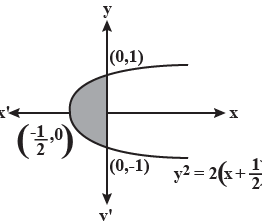
Question

The area (in sq unit) of the region bounded by the curves $2x = y^2 - 1$ and $x = 0$ is

• A. $\frac{1}{3}$
• B. $\frac{2}{3}$
• C. $1$
• D. $2$

Answer 1

Answer: (B)

Given curve can be rewritten as
$y ^{2}=2 x +\frac{1}{2}$
Therefore, required area $=\int\limits_{-1}^{1} xdy$
$=2 \int\limits_{0}^{1} \frac{ y ^{2}-1}{2} dy$
$=\left[\frac{ y ^{3}}{3}- y \right]_{0}^{1}$
$=\frac{1}{3}-1=\frac{2}{3}$ sq unit