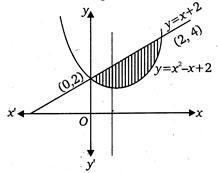
Q. The area enclosed between the parabola $ y={{x}^{2}}-x+2 $ and the line $ y=x+2 $ in sq unit equals
JamiaJamia 2008
Solution:
Given equation of parabola is
$ y={{x}^{2}}-x+2 $ Or $ {{\left( x-\frac{1}{2} \right)}^{2}}=y-\frac{7}{4} $ and equation of line is $ y=x+2 $ $ \therefore $ Required area $ =\int_{0}^{2}{[(x+2)-({{x}^{2}}-x+2)]}\,dx $ $ =\int_{0}^{2}{(-{{x}^{2}}+2x)}\,dx $ $ =\left[ -\frac{{{x}^{3}}}{3}+{{x}^{2}} \right]_{0}^{2}=-\frac{8}{3}+4 $ $ =\frac{4}{3} $ sq unit