Q.
The area enclosed between the curves $ y = ax^2 $ and
$ x = ay^2 (a>0) $ is 1 sq unit. Then, the value of a is
IIT JEEIIT JEE 2004
Solution:
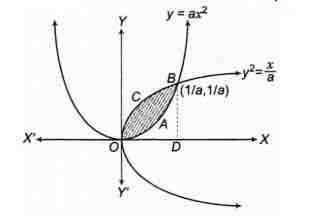
As from the figure, area enclosed between the curves is
OABCO.
Thus, the point of intersection of
$\, \, \, \, \, \, \, \, \, \, y = ax^2 $and $ x = ay^2 $
$ \Rightarrow \, \, \, \, \, \, \, \, \, x = a (ax^2)^2 $
$ \Rightarrow \, \, \, \, \, \, \, \, \, x = 0, \frac{1}{a} \Rightarrow y = 0, \frac{1}{a}$
So, the points of intersection are (0, 0) and $ \bigg(\frac{1}{a}, \frac{1}{a}\bigg)$
$ \therefore $ Required area OABCO = Area of curve OCBDO
- Area of curve OABDO
$ \Rightarrow \, \, \, \, \int \limits_0^{1/a} \bigg (\sqrt \frac{x}{a} - ax^2\bigg) dx = 1\, \, \, \, \, \, \, \, \, [given]$
$ \Rightarrow \bigg [ \frac{1}{\sqrt a}.\frac{x^{3/2}}{3/2} - \frac{ax^3}{3} \bigg]_0^{1/a} = 1$
$ \Rightarrow \, \, \, \, \, \, \frac{2}{3a^2} - \frac{1}{3a^2} = 1$
$ \Rightarrow \, \, \, \, \, \, \, \, \, \, \, \, a^2 = \frac{1}{3} \Rightarrow a = \frac{1}{\sqrt3}\, \, \, \, \, [\because a > 0] $