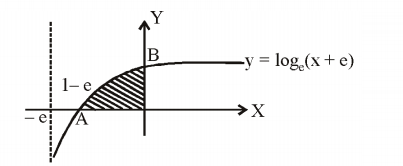
Q. The area enclosed between the curve $y = log_{e} (x+e)$ and the coordinate axes is
Application of Integrals
Solution:
Required area $\left(OAB\right)= \int\limits_{1-e}^{0} ln \left(x+e\right)dx $
$=\left[x ln \left(x+e\right)-\int \frac{1}{x+e} xdx \right]_{1-e}^{0} $
$=\left[\left(x+e\right)log \left(x+e\right)-x\right]_{1-e}^{0} =1 $