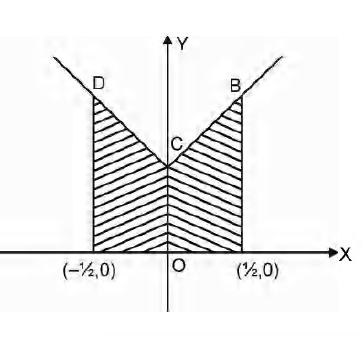
Q. The area bounded by y-1 =|x|, y=0 and $\left|x\right|$ =$\frac{1}{2}$ will be:
VITEEEVITEEE 2017
Solution:
The given lines are,
$y-1=x, x \geq 0 ; y-1=-x, x < 0$
$y=0 ; x=-\frac{1}{2}, x < 0 ; x=\frac{1}{2}, x \geq 0$
so that the area bounded is as shown in the figure.
Required area $=2 \int\limits_{0}^{1 / 2}(1+x) d x$
$=2\left(x+\frac{x^{2}}{2}\right)_{0}^{1 / 2}$
$=2\left(\frac{1}{2}+\frac{1}{8}\right)=\frac{5}{4}$