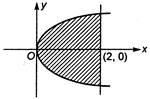
Q. The area bounded by the parabola $ {{y}^{2}}=8x $ and its latus rectum in sq unit is
Solution:
The given equation of parabola is
$ {{y}^{2}}=8x $ ...(i)
Required area
$=2\int_{0}^{2}{\sqrt{8x}}dx=2.2\sqrt{2}\int_{0}^{2}{\sqrt{x}}dx $
$=4\sqrt{2}\left[ \frac{{{x}^{3/2}}}{3/2} \right]_{0}^{2}=4\sqrt{2}\left[ \frac{2\sqrt{2}}{3/2} \right] $
$=\frac{32}{3}sq\,unit $