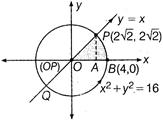
Q. The area bounded by the circle $ {{x}^{2}}+{{y}^{2}}=16 $ and the line $ y=x $ in the first quadrant is
J & K CETJ & K CET 2013Application of Integrals
Solution:
Given, circle is $ {{x}^{2}}+{{y}^{2}}=16 $ ..(i)
and line is $ y=x $ ..(ii)
On solving both equations, we get
$ {{x}^{2}}+{{x}^{2}}=16 $
$ \Rightarrow $ $ 2{{x}^{2}}=16\,\,\,\,\Rightarrow \,\,\,\,{{x}^{2}}=8 $
$ \Rightarrow $ $ x=\pm 2\sqrt{2} $
and $ y=\pm 2\sqrt{2} $
$ \therefore $ Intersection points are
$ P(2\sqrt{2},2\sqrt{2}) $
and $ Q(-2\sqrt{2},\,-2\sqrt{2}) $
$ \therefore $ Required area = Area of
$ \Delta OAP+ $ Area of $ \Delta APB $
$ =\frac{1}{2}\times OA+AP+\int_{2\sqrt{2}}^{4}{\sqrt{16-{{x}^{2}}}}\,\,dx $
$ =\frac{1}{2}\times 2\sqrt{2}\times 2\sqrt{2} $
$ +\left[ \frac{x}{2}\,\sqrt{16-{{x}^{2}}}+\frac{16}{2}{{\sin }^{-1}}\left( \frac{x}{4} \right) \right]_{2\sqrt{2}}^{4} $
$ =4+\left[ 0+8\times \frac{\pi }{2}-\sqrt{2}\times 2\sqrt{2}-8{{\sin }^{-1}}\left( \frac{1}{\sqrt{2}} \right) \right] $
$ =4+\left( 4\pi -4-8\times \frac{\pi }{4} \right) $
$ =4+(4\pi -4-2\pi ) $
$ =4+2\pi -4=2\pi $ sq units