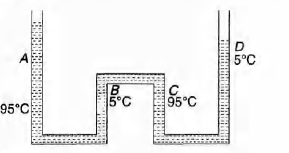
Q.
The apparatus shown in figure consists of four glass columns
connected by horizontal sections . The height of two central
connected B and C are 49 cm each. The two outer columns A
and D are open to the atmosphere .A and C are maintained at
a temperature of $95 ^{\circ}C$ while the columns B and D are
maintained at $5 ^{\circ}C$.The height of the liquid in A and D
measured from the base line are 52.8 am and 51 am
respectively.Determine the linear coefficient of thermal
expansion of the liquid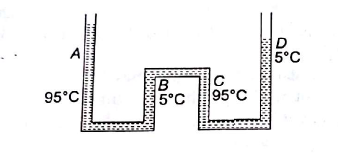
IIT JEEIIT JEE 1997Thermodynamics
Solution:
Density of a liquid varies with temperature as
$ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \rho_1 \,{}^{\circ}= \bigg(\frac{\rho _0 \,{}^{\circ}}{1+ \gamma t}\bigg)$
Here, $\gamma$ is the coefficient of volume expansion of
temperature
In the figure
$h_1=52.8 am , h_2 =51 cm \, and \, h=49 cm$
Now, pressure at B = pressure at C
$p_0+h_1 \rho_{95 ^{\circ}}g-h \rho_{5^\circ} g =p_0+h_2 \rho_{5^\circ} g- h\rho{95^\circ} g$
$\Rightarrow \, \, \, \, \, \, \rho_{95^{\circ}}(h_1+h ) =\rho _{5^{\circ}}(h_2 + h)0$
$\Rightarrow \, \, \, \, \, \frac{\rho_{95^{\circ}}}{\rho_{5^{\circ}}}= \frac{h_2+h}{h_1+h} \, \, \Rightarrow \, \, \, \, \frac{\frac{\rho_{0^\circ}}{1+95 \gamma}}{\frac{\rho_{0^\circ}}{1+5 \gamma}}=\frac{h_2+h}{h_1+h} $
$\Rightarrow \, \, \, \, \, \, \, \, \, \, \frac{1+5\gamma}{1+95 \gamma}=\frac{51+49}{52.8+49}=\frac{100}{101.8}$
Solving this equation, we get
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \gamma =2 \times 10^{-4} / ^{\circ}$
$\therefore \, \, \, $ Coefficient of linear expansion of temperature,
$ \, \, \, \, \, \, \, \, \alpha =\frac{\gamma}{3} 6.7 \times 10^{-5} / ^{\circ} C$