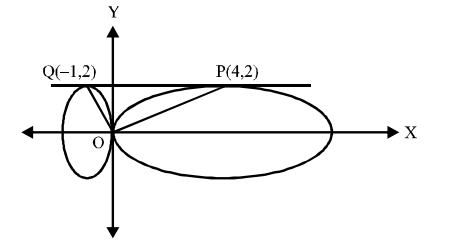
Q. The angle subtended by common tangents of two ellipses $4(x-4)^{2}+25 y^{2}=100$ and $4(x+1)^{2}+y^{2}=4$ at the origin is
Conic Sections
Solution:
$\frac{(x-4)^{2}}{25}+\frac{y^{2}}{4}=1$
and $(x-1)^{2}+\frac{y^{2}}{4}=1$
Clearly, $m_{O P} \cdot m_{O Q}=-1$
Therefore, $OP$ and $OQ$ are perpendicular to each other,