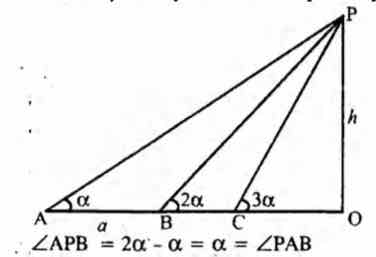
Q. The angle of elevation of the top of a T.V. Tower from three points A, B, C in a st. line through the foot of the tower are $\alpha, 2\alpha, 3\alpha$ respectively. If AB = $a$, the height of the tower is
Solution:
Let OP be a vertical tower. The elevation of top P from A, B, C are respectively $\alpha$ , 2$\alpha$ , 3$\alpha$ respectively.
From, rt. $\Delta d $ = OBP , $\frac{OP}{BP} $ = sin $2 \alpha$
$\therefore $ OP = BP sin $2 \alpha = a$ sin $2 \alpha$
Thus, height of the tower = $a$ sin $2 \alpha$.