Question

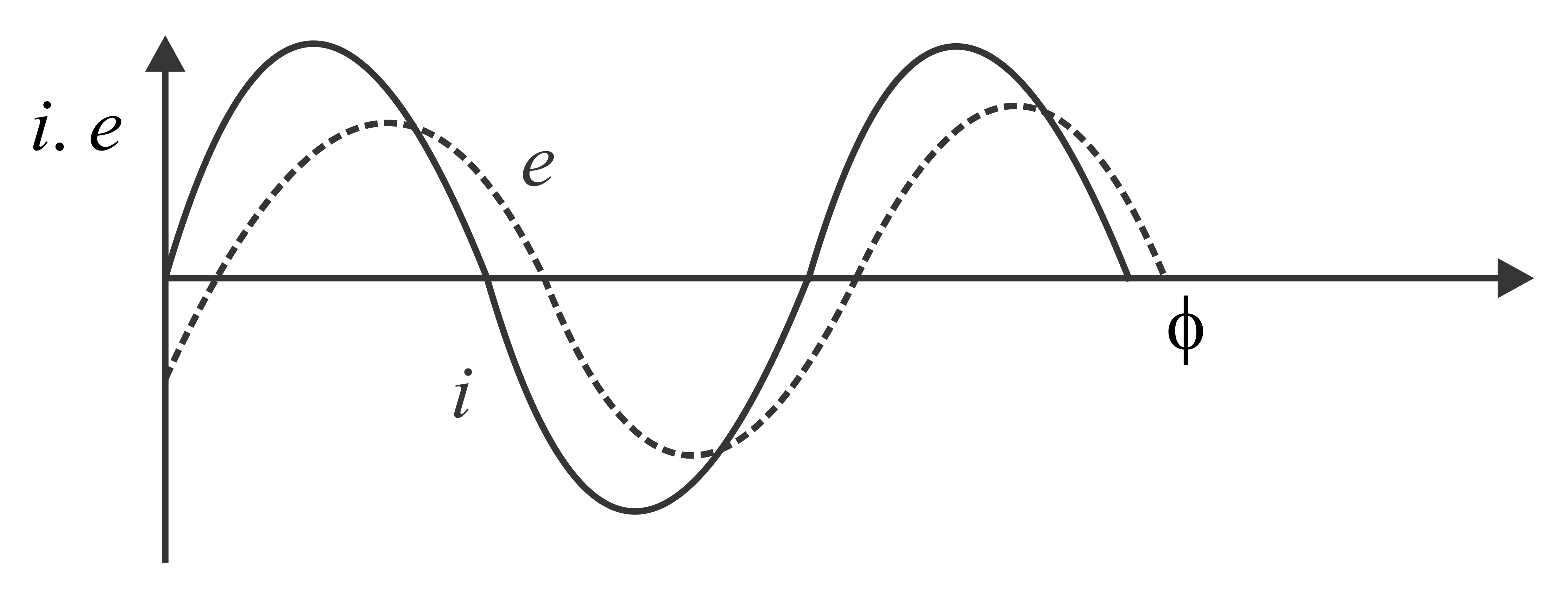
The adjoining diagram represents EMF $e$ and the current $I$ having a phase difference of $\frac{\pi }{4}$ in a circuit which has an AC source of emf $e=E_{0}sin\left(100 t\right)V$ connected across it. If the circuit only possibly consists of RC or RL or LC in series, then find the relation between the two possible elements of the circuit.

• A. $R=1\,k\Omega ,C=10\,μF$
• B. $R=1\,k\Omega ,C=1\,μF$
• C. $R=1\,k\Omega ,L=10\,H$
• D. $R=1\,k\Omega ,L=1\,H$

Answer 1

Answer: (A)

The current is leading the voltage in the given graph and the phase difference is not equal to $90^{0}$ . So, we can conclude that resistor and capacitor can be the probable elements of the circuit.
If we take $R$ to be the resistance and $C$ to be the capacitance and $\phi$ be the phase difference between current and applied voltage.
For RC circuit,
$ \, tan \, \phi=\frac{X_{c}}{R}$
For $\phi=45^{^\circ }$ , $tan\phi=1$
$\frac{X_{c}}{R}=1X_{c}=R\Rightarrow \frac{1}{\omega C}=R$
Given that, $R=1\,k\Omega ,\omega =100$
Substituting in the above equation, we get
$\frac{1}{100 C}=1\times 10^{3}C=10\,μF$