Q.
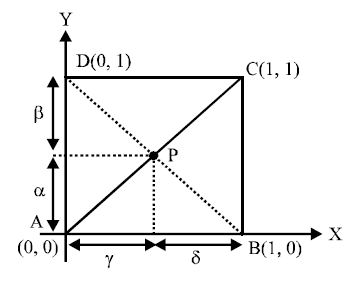
The $ABCD$ is a square with sides of unit length. Points $E$ and $F$ are taken on sides $AB$ and $AD$ respectively so that $AE = AF$. Let $P$ be a point inside the square $ABCD$.
The value of $( PA )^{2}-( PB )^{2}+( PC )^{2}-( PD )^{2}$ is equal to
Straight Lines
Solution:
$(P A)^{2}-(P B)^{2}+(P C)^{2}-(P D)^{2}$
$=\left(\alpha^{2}+\gamma^{2}\right) \left(\alpha^{2}+\delta^{2}\right)+\left(\delta^{2}+\beta^{2}\right)-\left(\gamma^{2}+\beta^{2}\right)=0$