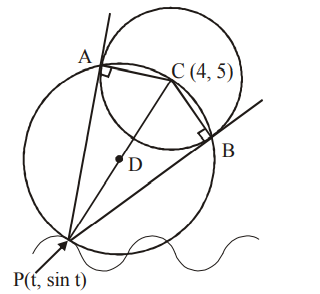
Question

Tangents $PA$ and $PB$ are drawn to the circle $( x -4)^{2}+$ $(y-5)^{2}=4$ from the point $P$ on the curve $y=\sin x$ where $A$ and $B$ lie on the circle. Consider the function $y=f(x)$ represented by the locus of the centre of the circumcircle of triangle $PAB$. Then answer the following questions.
The period of $y = f ( x )$ is

• A. $2 \pi$
• B. $3 \pi$
• C. $\pi$
• D. not defined

Answer 1

Answer: (C)

The center of the given circle is $C (4,5)$. Points $P , A , C$ and $B$ are concyclic such that $PC$ is the diameter of the circle. Hence the center D of the circumcircle of $\Delta ABC$ is the midpoint of $PC$.
Then, we have
$h =\frac{ t +4}{2} \text { and } k =\frac{\sin t -5}{2}$
Eliminating t, we have
$k=\frac{\sin (2 h-4)+5}{2}$
or $y=\frac{\sin (2 x-4)+5}{2}$
or $f^{-1}(x)=\frac{\sin ^{-1}(2 x-5)+4}{2}$
Thus, the range of
$y=\frac{\sin (2 x-4)+5}{2}$
is $[2,3]$ and the period is $\pi$.
Also, $f(x)=4$, i.e. $\sin (2 x-4)=3$ which has no real solutions.
For $f(x)=1, \sin (2 x-4)=-3$ which has no real solutions.
But range of $y=\frac{\sin ^{-1}(2 x-5)+4}{2}$ is $\left[-\frac{\pi}{4}+2, \frac{\pi}{4}+2\right]$