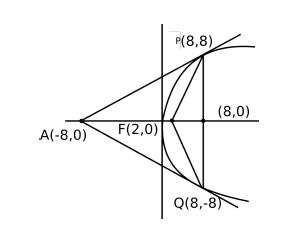
Q. Tangents drawn from the point $(-8, 0)$ to the parabola $y^2 = 8x$ touch the parabola at $P$ and $Q$ . If $F$ is the focus of the parabola, then the area of the triangle $PFQ$ (in sq. units) is equal to :
Solution:
Equation of tangent for parabola $y^{2} = 8x$
$y = mx+\frac{2}{m}$
tangent passing through $\left(-8, 0\right)$
$0 = -8m+\frac{2}{m}$
$m^{2} = \frac{1}{4}$
$m = \pm \frac{1}{2}$
for point $P\left(\frac{a}{m^{2}}, \frac{2a}{m}\right) = \left(\frac{2}{1/2}, \frac{4}{1/2}\right) = \left(8, 8\right)$
$Q\left(\frac{2}{1/4}, \frac{4}{-1/2}\right) = \left(8, -8\right)$
Area of $\Delta PFQ = \frac{1}{2}\times16\times6 = 48$ sq.units.