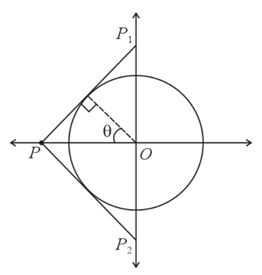
Question

Tangents are drawn to the circle $x^{2}+y^{2}=50$ from a point $'P'$ lying on the x-axis. These tangents meet the y-axis at points $'P_{1}'$ and $'P_{2}'$ . Possible coordinates of $'P'$ so that area of triangle $PP_{1}P_{2}$ is minimum, are

• A. $\left(10 ,0\right)$
• B. $\left(5 \sqrt{2} , 0\right)$
• C. $\left(5 ,0\right)$
• D. $\left(\frac{5}{\sqrt{2}} , 0\right)$

Answer 1

Answer: (A)

$OP=5\sqrt{2}sec \theta $
$OP_{1}=5\sqrt{2}cosec \, \theta $
area $\left(\Delta P P_{1} P_{2}\right)=\frac{100}{s i n 2 \theta }$
area $\left(\Delta P P_{1} P_{2}\right)_{m i n}=100\Rightarrow \theta =\pi /4\Rightarrow OP=10$
$P\left(10 , \, 0\right)\Rightarrow $ or $P\left(- 10 ,0\right)$
Hence $\left(A\right)$ is correct