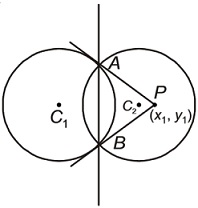
Question

Tangents are drawn to the circle $x^{2}+y^{2}=16$ at the points where it intersects the circle $x^{2}+y^{2}-6x-8y-8=0,$ then the point of intersection of these tangents is

• A. $\left(4 , \frac{16}{3}\right)$
• B. $\left(12 , 16\right)$
• C. $\left(3 , 4\right)$
• D. $\left(16 , 12\right)$

Answer 1

Answer: (B)

$S_{1}:x^{2}+y^{2}-16=0$
$S_{2}:x^{2}+y^{2}-6x-8y-8=0$
In this case, the common chord is the same as the chord of contact $AB$
So, the equation of $AB$ is $3x+4y-4=0$ which is identical with $xx_{1}+yy_{1}-16=0$
$\frac{x_{1}}{3}=\frac{y_{1}}{4}=\frac{16}{4}$
$\Rightarrow \, \, x_{1}=12, \, y_{1}=16$
$\Rightarrow \, P\left(x_{1} , y_{1}\right)=\left(12 , 16\right)$