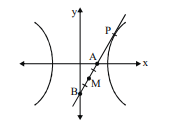
Question

Tangents are drawn from any point on the hyperbola $4 x^2-9 y^2=36$ to the circle $x^2+y^2-9=0$. If the locus of the midpoint of the chord of contact is $\left(\frac{x^2}{9}-\frac{y^2}{4}\right)=\lambda\left(\frac{x^2+y^2}{9}\right)^2$, then $\lambda$ is equal to

• A. 1
• B. 4
• C. 9
• D. 16

Answer 1

Answer: (A)

$ \frac{x^2}{9}-\frac{y^2}{4}=1, x^2+y^2=9$
Let $P(3 \sec \theta, 2 \tan \theta)$
From $P$, tangents $P A$ and $P B$ are drawn to circle $x^2+y^2=9$
$\therefore$ Equation of chord of contact $AB$ w.r.t. $P$ is $T =0$
$3 x \sec \theta+2 y \tan \theta=9$....(i)
Let Mid point of $A B$ is $M(h, k)$
$\therefore$ Equation of chord w.r.t. M
$T = S _1 $
$hx + ky -9= h ^2+ k ^2-9$.....(ii)
Compare (i) and (ii)
$T = S _1 $
$hx + ky -9= h ^2+ k ^2-9$
$ \frac{3 \sec \theta}{h}=\frac{2 \tan \theta}{k}=\frac{9}{h^2+k^2} \Rightarrow \sec \theta=\frac{h}{3}\left(\frac{9}{h^2+k^2}\right)$
$\text { and } \tan \theta=\left(\frac{k}{2}\right)\left(\frac{9}{h^2+k^2}\right) $
$\text { As, } \sec ^2 \theta-\tan ^2 \theta=1$

$\Rightarrow \left(\frac{h^2}{9}-\frac{k^2}{4}\right)=\left(\frac{h^2+k^2}{9}\right)^2$
$\therefore$ compare with $\left(\frac{ x ^2}{9}-\frac{ y ^2}{4}\right)=\lambda\left(\frac{ x ^2+ y ^2}{9}\right)^2$
\Rightarrow \lambda=1 $