Question

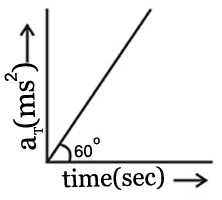
Tangential acceleration of a particle moving in a circle of radius $1 \, m$ varies with time $t$ as shown in figure (initial velocity of the particle is zero). Time after which total acceleration of particle makes an angle of $30^\circ $ with radial acceleration is

• A. $4s$
• B. $\frac{4}{3}s$
• C. $2^{2/3}s$
• D. $\sqrt{2}$ $s$

Answer 1

Answer: (C)

Given that $\frac{\text{a}_{\text{t}}}{\text{t}} = \text{tan 60}^{\text{o}}$
$\Rightarrow \quad a_t=\sqrt{3} \mathrm{t}$
$\frac{\text{dv}}{\text{dt}} = \sqrt{3} \text{t}$
$\Rightarrow \displaystyle \int _{0}^{\text{v}} \text{dv} = \sqrt{3} \text{t dt}$

$\text{v} = \frac{\sqrt{3} \text{t}^{2}}{2}$ ...(2)
Given that $\text{tan 30}^{\text{o}}=\frac{\text{a}_{\text{t}}}{\text{a}_{\text{c}}}\Rightarrow \frac{1}{\sqrt{3}}=\frac{\text{a}_{\text{t}}}{\text{a}_{\text{c}}}$
$\Rightarrow \text{a}_{\text{c}}=\sqrt{3}\text{a}_{\text{t}}$
$\frac{\mathrm{v}^2}{\mathrm{R}}=\sqrt{3} \mathrm{a}_{\mathrm{t}}$
From (1) and (2) $\frac{\left(\frac{\sqrt{3}}{2} t^2\right)^2}{1}=\sqrt{3} \times \sqrt{3} \mathrm{t} \quad \Rightarrow \quad \frac{3}{4} t^4=3 \mathrm{t}$
$\text{t}^{3} = 4$
$\Rightarrow \text{t} = 2^{2 / 3} \text{sec.}$