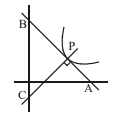
Question

Tangent to a non-linear curve $y=f(x)$ at any point $P$ intersect $x$-axis and $y$-axis at $A$ and $B$ respectively. If normal to the curve $y=f(x)$ at $P$ intersect $y$-axis at $C$ such that $A C=B C, f(2)=3$. Then equation of curve is

• A. $x y=6$
• B. $x^2+y^2=13$
• C. $2 y^2=9 x$
• D. $2 y=3 x$

Answer 1

Answer: (A)

Equation of tangent at $P \left( x _1, y _1\right)$
$y - y _1=\frac{ dy }{ dx }\left( x - x _1\right)$

$\Rightarrow A\left(\left(x_1-\frac{y_1}{\left(\frac{d y}{d x}\right)}\right), 0\right) $
$B\left(0, y_1-x_1 \frac{d y}{d x}\right)$
Equation of normal at $P \left( x _1, y _1\right)$
$ y - y _1=\frac{-1}{ dy / dx }\left( x - x _1\right) $
$C \left(0, \frac{ x _1}{ dy / dx }+ y _1\right)$
$\Theta AC = BC$
$\left( x _1-\frac{ y _1}{ dy / dx }\right)^2+\left(\frac{ x _1}{ dy / dx }+ y _1\right)^2=\left( y _1-\frac{ dy }{ dx } x _1-\frac{ x _1}{ dy / dx }- y _1\right)^2 $
$y _1= \pm x _1 \frac{ dy }{ dx } $
$\Rightarrow \int \frac{- dy }{ y }=\int \frac{ dx }{ x } \text { (positive sign give linear curve) } $
$\Rightarrow-\ln y =\ln x +\ln c \Rightarrow xy = c $
$\therefore f (2)=3 \Rightarrow xy =6 $