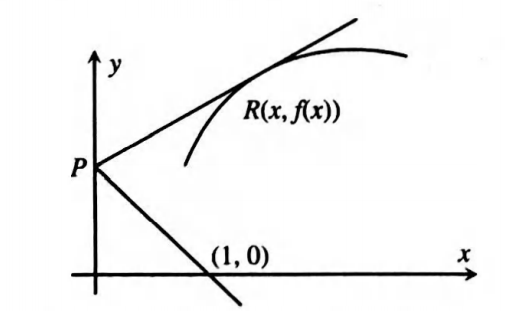
Question

Tangent to a curve intercepts the $y$-axis at a point $P$. A line perpendicular to this tangent through $P$ passes through another point $(1,0)$ . The differential equation of the curve is

• A. $y \frac{d y}{d x}-x\left(\frac{d y}{d x}\right)^{2}=1$
• B. $\frac{x d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{2}=0$
• C. $y \frac{d x}{d y}+x=1$
• D. None of these

Answer 1

Answer: (A)

The equation of the tangent at the point
$R(x, f(x))$ is $Y-f(x)=f'(x)(X-x)$

The coordinates of the point $P$ are $\left(0, f(x)-x f'(x)\right)$
The slope of the perpendicular line
through $P$ is $\frac{f(x)- xf'(x)}{-1} = - \frac{1}{f'x} $
$\Rightarrow f(x) f'(x)-x\left(f'(x)\right)^{2}=1$
$\Rightarrow \frac{y d y}{d x}-x\left(\frac{d y}{d x}\right)^{2}=1$
which is required differential equation to the curve at $y=f(x)$