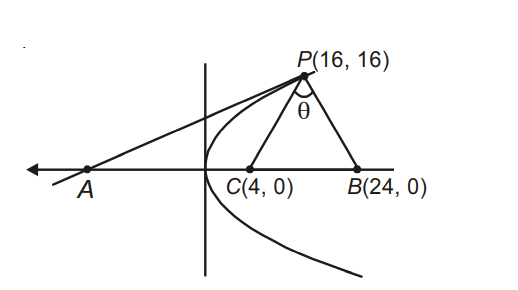
Q. Tangent and normal are drawn at $P(16, 16)$ on the parabola $y^2 = 16x$, which intersect the axis of the parabola at $A$ and $B$, respectively. If $C$ is the centre of the circle through the points $P, A$ and $B$ and $\angle CPB = \theta$, then a value of $\tan \, theta$ is:
Solution: