Question

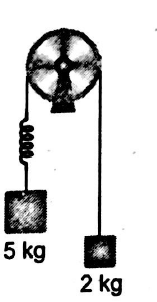
System shown in the figure is released from rest with mass $2 \,kg$ in contact with ground. Pulley and spring are massless and the friction is absent everywhere. The speed of $5 \,kg$ block when $2\, kg$ block leaves the contact with the ground is (force constant of spring $k=40 \,Nm ^{-1}$ and $\left.g=10\, ms ^{-2}\right)$

• A. $ \sqrt{2}\,m{{s}^{-1}} $
• B. $ 2\sqrt{2}\,m{{s}^{-1}} $
• C. $ 2\,m{{s}^{-1}} $
• D. $ 4\sqrt{2}\,m{{s}^{-1}} $

Answer 1

Answer: (B)

Let $x$ be the extension in the string when $2 \,kg$ block leaves the contact with ground. Then tension in the spring should be equal to weight of $2\, kg$ block.
$k x=2\, g $ or $x=\frac{2 g}{k}=\frac{2 \times 10}{40}=\frac{1}{2}\, m$
Now, from conservation of mechanical energy
$m g x=\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2} $
Or $ v=\sqrt{2 g x-\frac{k x^{2}}{m}} $
$=\sqrt{2 \times 10 \times \frac{1}{2}-\frac{40}{4 \times 5}} $
$=2 \sqrt{2} \,m s^{-1}$