Question

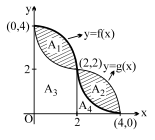
Suppose $y=f(x)$ and $y=g(x)$ are two continuous functions whose graphs intersect at the three points $(0,4),(2,2)$ and $(4,0)$ with $f ( x )> g ( x )$ for $0< x <2$ and $f ( x )< g ( x )$ for $2< x < 4$. If $\int\limits_0^4[f(x)-g(x)] d x=10$ and $\int\limits_2^4[g(x)-f(x)] d x=5$, the area between two curves for $0

• A. 5
• B. 10
• C. 15
• D. 20

Answer 1

Answer: (C)

Given $\int\limits_0^4 f(x) d x-\int\limits_0^4 g(x) d x=10 $
$\left( A _1+ A _3+ A _4\right)-\left( A _2+ A _3+ A _4\right)=10 $
$A _1- A _2=10 \text {....(1) } $
$\text { again } \int\limits_2^4 g(x) d x-\int\limits_2^4 f(x) d x=5$
$\left( A _2+ A _4\right)- A _4=5 $
$A _2=5$ ....(2)
$\therefore \quad(1)+(2)$
$ A _1=15$