Q.
Suppose two planets (spherical in shape) of radii $R$ and $2R$, but mass $M$ and $9\, M$ respectively have a centre to centre separation $8\, R$ as shown in the figure. A satellite of mass ' $m$ ' is projected from the surface of the planet of mass '$M$' directly towards the centre of the second planet. The minimum speed '$v$' required for the satellite to reach the surface of the second planet is $\sqrt{\frac{a}{7} \frac{ GM }{R}}$ then the value of '$a$' is_____
[Given: The two planets are fixed in their position]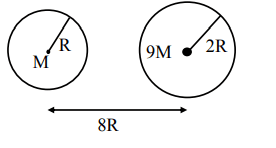
Solution:
